SIMULATION TOOLS: The BERGulator
(BERG = Cornell University Blind Equalization Research Group)
Download the most recent version of the BERGulator (.tar.gz)
Download the most recent version of the BERGulator (.zip)
(The most recent version of the BERGulator is dated
Sun Aug 19 10:08 EDT 2001.
It includes .mexlx files for Linux-based systems and a workaround for
some Matlab-6 bugs. You may compile the *.c files yourself for other
platforms using matlab's "mex" command.)
The BERGulator is a MATLAB5-based interactive simulation tool aimed
at studying the behavior of the Constant Modulus Algorithm
(CMA) when used for direct blind linear channel equalization.
The BERGulator allows you to specify the channel impulse response
coefficients, the level of channel noise, and the source alphabet
used for experimentation. The channel may be complex-valued, and
complex-valued noise is assumed if either the source or the channel
is complex-valued. Furthermore, the channel may be baud-spaced or
T/2 fractionally-spaced.
Given such a channel/noise combination, The BERGulator is capable of
plotting the frequency/impulse responses of the channel, the MMSE
optimal equalizer, and the optimal system (chan+eq). For length-2
real-valued channels, it can also plot contours of the CMA surface
in equalizer space (with an overlay of the principle axes of the
quadratic-cost ellipsoid approximating the neighborhoods of CM minima,
and with *'s and x's indicating the locations of MMSE and MSE minima).
When a valid surface is present, The BERGulator can superimpose the
CM-error-function sign-boundaries (for real-valued sources) and
indicate the magnitude and direction of the (constant) cost-gradient
within a given constant-sign region. This feature is motivated by
the convergence behavior of signed algorithms.
Finally, the BERGulator can plot the tap-trajectories of an equalizer
adaptation algorithm and plot the CM- and mean-squared error
histories. When an error surface is present and the tap-trajectories
will be real-valued, the user can select the equalizer intialization
from the surface and the resulting trajectory will be superimposed on
it. For higher-dimensional and/or complex-valued equalizers, the user
selects the location of a single/double spike (BSE/FSE) initialization.
The equalizer-length, stepsize, and the number of iterations can be
varied. Numerous variants of the CMA algorithm are available for
experimentation.
After simulation run has completed, the frequency/impulse response
of any equalizer along the adaptation history can be displayed.
In addition the selected equalizer, the local MMSE equalizer, the
corresponding system response and the local MMSE system response are
also displayed. If a surface trajectory is present, this equalizer
selection is obtained from the surface. If only the coefficient
history is present, this equalizer is selected from a selected point
in the adaptation history. A round/diamond marker is then placed on
graph to indicate a frequency/impulse response analysis.
When parameter changes are made that invalidate the currently
displayed frequency/impulse responses or error surface, the
offending object is automatically erased. On the contrary, any
analyses based on an simulation run is retained (for comparison to
other experiments) until the "Clear Traces" button is pressed.
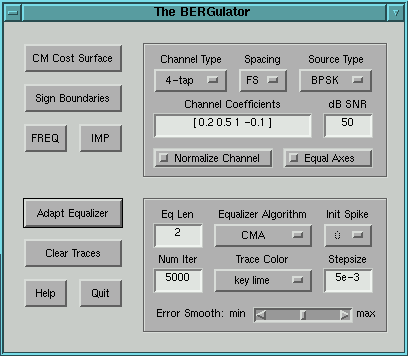
Actions
- CM Cost Surface: Plots contours of the Godard 2-2 cost surface in eq space
- Sign Boundaries: Overlays CM-error-function sign-boundaries on surface
- Facet Gradients: Displays the 2D gradient of the signed-Godard cost surface
- FREQ: Frequency response analysis
- IMP: Impulse response analysis
- Adapt Equalizer: Runs a simulation using the selected parameters
- Clear Traces: Erases all adaptation-based tap/error/freq/imp-rspn traces
- Help: Prints help screen.
- Quit: Quit!
Channel Options
- Channel Type: Offers a choice between preselected channel coefficients,
user-selectable ("custom") ones, and ".mat" file input
where the coefs must be stored in a vector named "c"
- Source Type: A choice between a number of QAM and PAM source alphabets
- Spacing: T/2 Fractionally-spaced (FS) or Baud-spaced (BS)
- dB SNR: Signal-to-AWGN level in decibels
- Normalize Channel: Normalizes the channel coeficient vector (to unit norm)
- Equal Axes : Forces the surface plot x/y-axes to be equally scaled
(unfortunately this interferes with zooming)
Equalizer Algorithms
- CMA: The Godard 2-2 constant modulus algorithm
- N-CMA: Normalized CMA
- SE-CMA: Signed-error CMA (i.e. Godard 1-1)
- SR-CMA: Signed-regressor CMA
- SS-CMA: Signed-error, signed-regressor CMA
- DSE-CMA: Dithered signed-error CMA
- WSGA: "Signed Godard Algorithm" (Weerackody)
- CMA-GD: Godard 2-2 gradient descent (i.e. CMA avg-system behavior)
Algorithm Options
- Eq Len: The number of coefficients in the equalizer
- Init Spike: The T-spaced location of single/double spike initialization
for BS/FS equalizers
- Num Iter: The number of (baud-spaced) symbols used in the adaptation
- Trace Color: The color of the trace used to display tap/error histories
and frequency/impulse response analysis
- Stepsize: The stepsize used by the coefficient update algorithm
- Error Smooth: The amount of smoothing performed on the CM error history
(min = no smoothing)
The BERGulator keeps all variables local in scope unless the user
invokes the program "berg_global.m". In the latter case, the important
variables and user-interface handles are made available to the user
so that he/she/it may access these quantites and/or construct an
m-file automating the BERGulator user-interface.
Misc
- the T/2 implementation samples on "odd" outputs (assume {0,1,2,...})
when the equalizer length is even and "even" outputs when the equalizer
length is odd
- all "local-MSE" quantities are calculated based on the delay and phase
obtained from the maximum-magnitude entry of the latest simulation's
final system response
- the error-trace smoothing uses a 2nd-order butterworth filter
all signed CMA algorithms (except WSGA) compute the sign of a
complex number as the sign of the real part plus sqrt(-1) times
the sign of the imaginary part
BERGulator written by: Phil Schniter, June 1997
Send comments, bug reports, or cold hard cash to
schniter@ee.eng.ohio-state.edu.

