EM-NN-AMP Algorithm: A succinct overview
Jeremy Vila, Oct. 2013
EM-NN-AMP attempts to recover a sparse signal of length N through (possibly) noisy measurements of length M (with perhaps M < N). We model this through the linear system
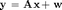 .
.
We focus on non-negative (NN) signals that obey the linear equality constraints
 .
.
EM-NN-AMP is comprised of three different algorithms: NN least-squares AMP (NNLS-AMP), expectation maximization NN LASSO AMP (EM-NNL-AMP), and EM NN Gaussian mixture AMP (EM-NNGM-AMP). Toggling between them using the EMNNAMP Matlab code is extremely easy.
Refer to the paper EM-NN-AMP by Jeremy Vila Philip Schniter for a detailed description of the algorithm. This manual will show how to use the EM-NN-AMP MATLAB code.
Contents
Example 1: Non-negative Uniform Data
The following example will use randomly generated data drawn from a uniform distribution
close all clear all N = 500; %Fix dimension of signal M = 1000; %Fix number of measurements SNR = 30; %Fix signal to noise ratio % Form A matrix from i.i.d. Gaussian entries % Generate normalized random sensing matrix Amat = randn(M,N); columnNorms = sqrt(diag(Amat'*Amat)); Amat = Amat*diag(1 ./ columnNorms); %unit norm columns A = MatrixLinTrans(Amat); %Generate non-sparse uniform signal x = rand(N,1); %Compute true noiseless measurement ztrue = A.mult(x); %Output channel- Calculate noise level muw = norm(ztrue)^2/M*10^(-SNR/10) %Compute noisy output y = ztrue + sqrt(muw)*(randn(M,1));
EM-NN-AMP is comprised of the NNLS-AMP, EM-NNL-AMP, and EM-NNGM-AMP algorithms. Toggling between them is straightforward. To run each algorithm on its defaults, all one needs to supply are the measurements and mixing matrix (or operator). The algorithm then returns the recovered linearly-constrained non-negative signal.
time = tic; optALG.alg_type = 'NNLSAMP'; %Pick the NNLS-AMP algorithm xhat = EMNNAMP(y, A, optALG); %Perform EMNNAMP time = toc(time) %Calculate total time
time =
0.2637
Verify accuracy of signal recovery with NMSE and plots
nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report NNLSAMP's NMSE (in dB) figure(1) plot(x,'b+');hold on %Plot true signal plot(xhat,'ro'); hold off %Plot signal estimates xlabel('Signal Index'); ylabel('Value') title('Case 1: Real Bernoulli-Gaussian Signal, Med Sparsity, High SNR') legend('True signal', 'Est Signal')
nmse = -30.1565
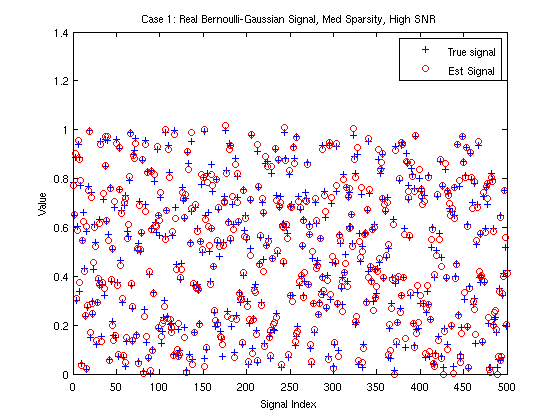
It is straightforward to run EM-NNL-AMP and EM-NNGM-AMP using the EMNNAMP Matlab code. Moreover, parameter initialization and learning are handled automatically.
Run EM-NNL-AMP
time = tic; optALG.alg_type = 'NNLAMP'; %Pick the EM-NNL-AMP algorithm xhat = EMNNAMP(y, A, optALG); %Perform EMNNAMP time = toc(time) %Calculate total time nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report NNLSAMP's NMSE (in dB)
time =
0.1077
nmse =
-29.2548
Run EM-NNGM-AMP
time = tic; optALG.alg_type = 'NNGMAMP'; %Pick the EM-NNGM-AMP algorithm xhat = EMNNAMP(y, A, optALG); %Perform EMNNAMP time = toc(time) %Calculate total time nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report NNLSAMP's NMSE (in dB)
time =
0.6455
nmse =
-30.2019
Alternatively, one can call xhat = EMNNAMP(y, A), as EMNNAMP assumes optALG.alg_type = 'NNGMAMP'; as the default
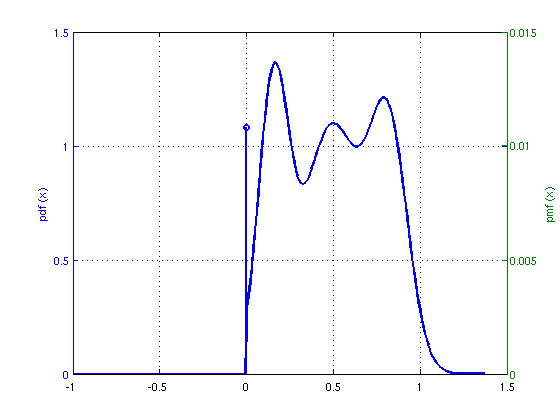
time = tic; [xhat,stateFin] = EMNNAMP(y, A); %Perform EMNNAMP time = toc(time) %Calculate total time nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report NNLSAMP's NMSE (in dB) % It is straightforward plot the recovered NNGM signal distribution figure(2) plot_NNGM(stateFin);
time =
0.5392
nmse =
-30.2019
Example 2: Enforcing linear equality constraints
EM-NN-AMP can also handle other signal types including those with linear equality constraints, even in the compressive sensing regime.
clear('optALG'); %clear previous optALG options N = 500; %Fix dimension of signal del = 0.5; %undersampling ratio del = M/N rho = 0.3; %normalized sparsity rate rho = K/M SNR = 40; %Signal to noise ratio (dB) M = ceil(del*N); %Find appropriate measurement size K = floor(rho*M); %Find appropriate sparsity if K == 0 K = 1; %Ensure at least one active coefficient. end % Form A matrix %Generate normalized random sensing matrix Amat = randn(M,N); columnNorms = sqrt(diag(Amat'*Amat)); Amat = Amat*diag(1 ./ columnNorms); %unit norm columns A = MatrixLinTrans(Amat); %Generate signal x = dirrnd(10*ones(1,K),1)'; x(end+1:N) = zeros(N-K,1); x = x(randperm(N)); %Compute true noiseless measurement ztrue = A.mult(x); %Output channel- Calculate noise level muw = norm(ztrue)^2/M*10^(-SNR/10); %Compute noisy output y = ztrue + sqrt(muw)*(randn(M,1)); time = tic; optALG.linEqMat = ones(1,N); %supply linear equality matrix B optALG.linEqMeas = 1; %supply linear equality "measurement" c xhat = EMNNAMP(y, A, optALG); %Perform EM-NNGM-AMP time5 = toc(time) %Calculate total time nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) %Report recovery nmse in dB LE_nmse = 10*log10(norm(1-sum(xhat))^2) %Report the nmse of linear equality constraint
time5 =
0.7370
nmse =
-43.6912
LE_nmse =
-81.0532
Example 3: Real NN satellite image in compressive sensing regime
It is straightforward to apply EMNNAMP to real NN datasets. In this example, we recover a sparse NN image of a satellite under noisy, compressed linear measurements using the randomly row-sampled Hadamard transform operator.
clear('optEM') %clear previous options %load image and plot it load('satimage.mat','x') figure(3) imagesc(x); colormap('gray') title('True image') %Find dimension of signal and vectorize it N = numel(x); x = reshape(x,N,1); del = 0.3; %del = M/N SNR = 60; %Define SNR %Specify number of measurements M = ceil(del*N); %Build ``wide'' fast Walsh-Hadamard transform A = FWHTLinTrans(N,[],1); %get indeces of rows randomly ind = A.ySamplesRandom(M); %subsample by either method A.ySamplesSetFromSubScripts(ind); ztrue = A.mult(x); %Generate measurements muw = norm(ztrue)^2/M*10^(-SNR/10); %Calculate noise level y = ztrue + sqrt(muw)*randn(M,1); %Compute noisy output tstart = tic; optEM.maxEMiter = 20; %decrease maximum EM iterations optGAMP.adaptStep = false; %Turn off adaptive step size optGAMP.verbose= true; %Turn on GAMP verbosity xhat = EMNNAMP(y, A,[],optEM,optGAMP); %Perform EMNNGMAMP time = toc(tstart) nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report EMNNAMP's NMSE (in dB) %plot the recovered image figure(4) xhat = reshape(xhat,sqrt(N),sqrt(N)); imagesc(xhat) colormap('gray') title('Recovered image')
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 8.9293e-01
it= 3 value= -Inf step=1.000000 |dx|/|x|= 4.5428e-01
it= 4 value= -Inf step=1.000000 |dx|/|x|= 3.2736e-01
it= 5 value= -Inf step=1.000000 |dx|/|x|= 3.3032e-01
it= 6 value= -Inf step=1.000000 |dx|/|x|= 2.4342e-01
it= 7 value= -Inf step=1.000000 |dx|/|x|= 1.9355e-01
it= 8 value= -Inf step=1.000000 |dx|/|x|= 1.3773e-01
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 9.1461e-02
it= 3 value= -Inf step=1.000000 |dx|/|x|= 6.1167e-02
it= 4 value= -Inf step=1.000000 |dx|/|x|= 3.7276e-02
it= 5 value= -Inf step=1.000000 |dx|/|x|= 2.3354e-02
it= 6 value= -Inf step=1.000000 |dx|/|x|= 1.4662e-02
it= 7 value= -Inf step=1.000000 |dx|/|x|= 9.7413e-03
it= 8 value= -Inf step=1.000000 |dx|/|x|= 6.2188e-03
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 1.4732e-02
it= 3 value= -Inf step=1.000000 |dx|/|x|= 1.0989e-02
it= 4 value= -Inf step=1.000000 |dx|/|x|= 7.1601e-03
it= 5 value= -Inf step=1.000000 |dx|/|x|= 4.5972e-03
it= 6 value= -Inf step=1.000000 |dx|/|x|= 3.0652e-03
it= 7 value= -Inf step=1.000000 |dx|/|x|= 2.0099e-03
it= 8 value= -Inf step=1.000000 |dx|/|x|= 1.3768e-03
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 9.4657e-03
it= 3 value= -Inf step=1.000000 |dx|/|x|= 5.5721e-03
it= 4 value= -Inf step=1.000000 |dx|/|x|= 3.4097e-03
it= 5 value= -Inf step=1.000000 |dx|/|x|= 2.0678e-03
it= 6 value= -Inf step=1.000000 |dx|/|x|= 1.2475e-03
it= 7 value= -Inf step=1.000000 |dx|/|x|= 7.6485e-04
it= 8 value= -Inf step=1.000000 |dx|/|x|= 4.6673e-04
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 3.5261e-03
it= 3 value= -Inf step=1.000000 |dx|/|x|= 2.1794e-03
it= 4 value= -Inf step=1.000000 |dx|/|x|= 1.3361e-03
it= 5 value= -Inf step=1.000000 |dx|/|x|= 8.4048e-04
it= 6 value= -Inf step=1.000000 |dx|/|x|= 4.9564e-04
it= 7 value= -Inf step=1.000000 |dx|/|x|= 3.4642e-04
it= 8 value= -Inf step=1.000000 |dx|/|x|= 2.0818e-04
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 1.9695e-03
it= 3 value= -Inf step=1.000000 |dx|/|x|= 1.5375e-03
it= 4 value= -Inf step=1.000000 |dx|/|x|= 9.6826e-04
it= 5 value= -Inf step=1.000000 |dx|/|x|= 6.3375e-04
it= 6 value= -Inf step=1.000000 |dx|/|x|= 3.8093e-04
it= 7 value= -Inf step=1.000000 |dx|/|x|= 2.6926e-04
it= 8 value= -Inf step=1.000000 |dx|/|x|= 1.6186e-04
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 1.5145e-03
it= 3 value= -Inf step=1.000000 |dx|/|x|= 8.9954e-04
it= 4 value= -Inf step=1.000000 |dx|/|x|= 5.4786e-04
it= 5 value= -Inf step=1.000000 |dx|/|x|= 3.5647e-04
it= 6 value= -Inf step=1.000000 |dx|/|x|= 2.0569e-04
it= 7 value= -Inf step=1.000000 |dx|/|x|= 1.4300e-04
it= 8 value= -Inf step=1.000000 |dx|/|x|= 8.3166e-05
it= 1 value= -Inf step=1.000000 |dx|/|x|= NaN
it= 2 value= -Inf step=1.000000 |dx|/|x|= 5.2935e-04
it= 3 value= -Inf step=1.000000 |dx|/|x|= 2.8984e-04
it= 4 value= -Inf step=1.000000 |dx|/|x|= 1.7709e-04
it= 5 value= -Inf step=1.000000 |dx|/|x|= 1.0634e-04
it= 6 value= -Inf step=1.000000 |dx|/|x|= 6.2936e-05
it= 7 value= -Inf step=1.000000 |dx|/|x|= 3.7145e-05
it= 8 value= -Inf step=1.000000 |dx|/|x|= 2.2146e-05
time =
3.8528
nmse =
-61.6856


Example 4: Using the Laplacian noise model
EM-NN-AMP can assume an additive white Laplacian noise model for improved robustness to the outliers in the measurements.
clear('optALG'); %clear previous optALG options N = 1000; %Define signal dimension M = 1000; %Define number of measurements SNR = 20; %Define signal to noise ratio in dB % Form A matrix from i.i.d. Gaussian entries % Generate normalized random sensing matrix Amat = randn(M,N); columnNorms = sqrt(diag(Amat'*Amat)); Amat = Amat*diag(1 ./ columnNorms); %unit norm columns A = MatrixLinTrans(Amat); %Define signal as a truncated Gaussian. x = randn(N,1); x(x<0) = 0; ztrue = A.mult(x); %Form noiseless measurements muw = norm(ztrue)^2/M*10^(-SNR/10); %Calculate noise level y = ztrue + sqrt(muw)*(randn(M,1)); %Compute noisy output ind = randperm(N,4); %select four indices to corrupt; y(ind) = ztrue(ind) + 5*randn(4,1); %Corrupt these indeces with outliers
Perform EMNNGMAMP without laplacian noise model
time = tic;
optALG.laplace_noise = false;
xhat = EMNNAMP(y, A, optALG);
time = toc(time)
nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report EMGMAMP's NMSE (in dB)
time =
1.1645
nmse =
-5.8222
Perform EMNNGMAMP with laplacian noise model
time = tic;
optALG.laplace_noise = true;
xhat = EMNNAMP(y, A, optALG);
time = toc(time)
nmse = 10*log10(norm(x-xhat)^2/norm(x)^2) % Report EMGMAMP's NMSE (in dB)
time =
1.9310
nmse =
-17.0440