EM-GM-AMP Algorithm: Usage Examples
Jeremy Vila and Philip Schniter, Nov. 2015
EM-GM-AMP attempts to recover a sparse signal of length N through (possibly) noisy measurements of length M (with perhaps M < N). We model this through the linear system
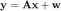 .
.
Please refer to the paper EM-GM-AMP by Jeremy Vila Philip Schniter for a detailed description of the algorithm. This manual will show how to use the EM-GM-AMP MATLAB code and how to intepret the results.
Contents
Generating Data
The following examples will use randomly generated data. First, we create the K-sparse signal, then the M-by-N measurement matrix, and finally the AWGN-corrupted measurements.
close all clear all % Check that EMGMAMP.m is on the path if exist('EMGMAMP.m')~=2 error('EMGMAMP.m not on the path') end % Choose between the new and old versions of EMGMAMP newEM = true; EMGMpath = fileparts(which('EMGMAMP')); % current path to EMGM [GAMPdir,EMGMver] = fileparts(EMGMpath); % GAMPmatlab dir and EMGM version if newEM if strcmp(EMGMver,'EMGMAMP') rmpath(EMGMpath) addpath([GAMPdir,'/EMGMAMPnew']) warning('Changing path from old to new version of EMGMAMP') end else if strcmp(EMGMver,'EMGMAMPnew') rmpath(EMGMpath) addpath([GAMPdir,'/EMGMAMP']) warning('Changing path from new to old version of EMGMAMP') end end % Handle random seed if verLessThan('matlab','7.14') defaultStream = RandStream.getDefaultStream; else defaultStream = RandStream.getGlobalStream; end; if 1 % use new random seed savedState = defaultStream.State; save random_state.mat savedState; else % reuse old random seed load random_state.mat end defaultStream.State = savedState; % Declare dimensions N = 5000; % signal length del = 0.4; % measurement-to-signal ratio, M/N rho = 0.4; % sparsity-to-measurement ratio, K/M SNR = 30; % SNR (in dB) M = ceil(del*N); % measurement length K = floor(rho*M); % sparsity if K==0 K = 1; % ensure at least one active coefficient end % Generate matrix clear Params Params.M = M; Params.N = N; Params.realmat = true; % specify real-valued matrix Params.type = 1; % specify i.i.d. Gaussian matrix Amat = generate_Amat(Params); % generate random matrix % Generate sparse signal active_mean = 1; % mean of non-zero components active_var = 1; % variance of non-zero components xtrue = zeros(N,1); % initialize signal vector xtrue(randperm(N,K)) = (sqrt(active_var)*randn(K,1)+active_mean); % Generate noisy outputs ztrue = Amat*xtrue; % compute true output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output
The Standard Way to Invoke EM-GM-AMP
Using the EM-GM-AMP algorithm is extremely easy. You simply need the measurements and measurement matrix. The algorithm returns signal estimate, the learned parameters of the assumed Gaussian-Mixture prior, as well as the AWGN variance.
% Run, time, and check performance of EMGMAMP optEM.heavy_tailed = false; % since operating on a sparse signal time = tic; [xhat, EMfin] = EMGMAMP(y, Amat, optEM); time = toc(time) NMSE_dB = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) wvar_error_dB = 10*log10(EMfin.noise_var/wvar)
time =
2.4293
NMSE_dB =
-29.9480
wvar_error_dB =
-0.0335
Plot the estimated distribution
figure(1) plot_GM(EMfin);
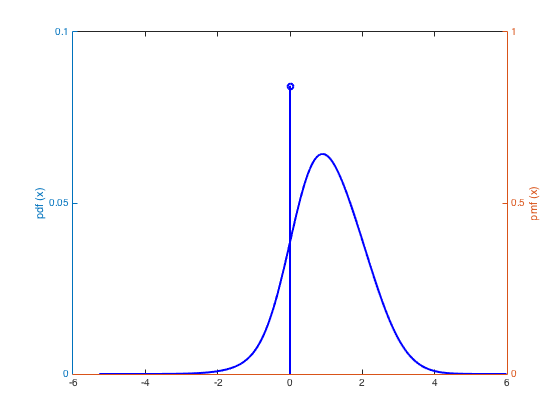
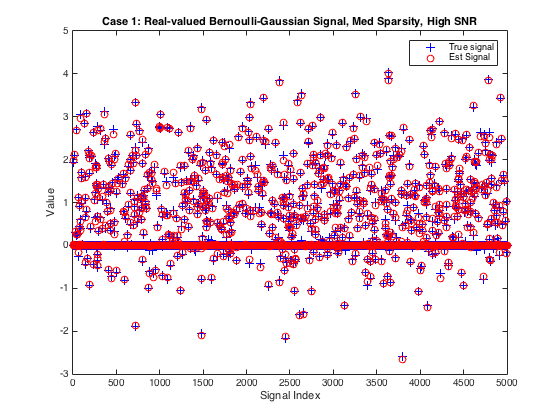
Plot the true and estimated signals
figure(2) plot(xtrue,'b+');hold on % plot true signal plot(xhat,'ro'); hold off % plot signal estimate xlabel('Signal Index'); ylabel('Value') title('Case 1: Real-valued Bernoulli-Gaussian Signal, Med Sparsity, High SNR') legend('True signal', 'Est Signal')
Exploiting Prior Signal Knowledge with EM-GM-AMP
Sometimes one has partial knowledge of the signal prior. To exploit this, we can disable the EM learning on one or more parameters.
% Set initial GM parameters at the true values clear optEM optEM.active_mean = 1; %Initialize at correct active mean optEM.active_weights = 1; %Trivial weights since 1-term "mixture" optEM.active_var = 1; %Initialize correct active variance optEM.noise_var = wvar; %Initialize at correct noise variance % Turn off EM learning of all but the sparsity-rate, lambda optEM.learn_lambda= true; optEM.learn_mean = false; optEM.learn_weights = false; optEM.learn_var = false; optEM.learn_noisevar = false; % Run, time, and check performance of EMGMAMP optEM.heavy_tailed = false; % since operating on a sparse signal time2 = tic; [xhat,EMfin] = EMGMAMP(y, Amat,optEM); time2 = toc(time2) NMSE_dB2 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) sparsity_error_dB = 10*log10(EMfin.lambda/(K/N))
time2 =
0.5919
NMSE_dB2 =
-29.9516
sparsity_error_dB =
0.0030
Using the Robust Mode of EM-GM-AMP and Showing the Convergence History
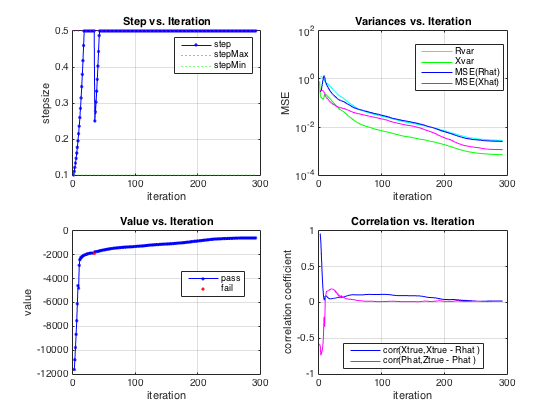
For non-iid measurement matrices, we suggest using EMGMAMP's "robust_gamp" mode. Below we generate a matrix with correlated columns, run EMGMAMP, and show the resulting convergence history. Notice how the damping parameter (i.e., the "stepsize") decreases when the utility function (i.e., the "value") decreases, to help the algorithm converge.
% Generate matrix clear Params Params.M = M; Params.N = N; Params.type = 1; Params.realmat = true; Params.tau = 0.7; % Make columns correlated Amat = generate_Amat(Params); % Generate the random matrix % Generate noisy outputs ztrue = Amat*xtrue; % compute true transform-output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output % Run, and check performance of EMGMAMP clear optEM optEM.robust_gamp = true; % help robustify the convergence optEM.heavy_tailed = false; % since operating on a sparse signal [xhat,~,estHist,~,optGAMPfin] = EMGMAMP(y, Amat, optEM); NMSE_dB4 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) % Show convergence history figure(3) gampShowHist(estHist,optGAMPfin,xtrue,ztrue);
NMSE_dB4 = -24.6896
Example 3: Real Bernoulli Signal
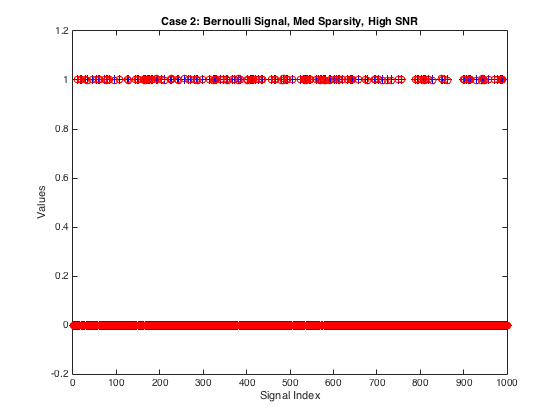
Let's see if EM-GM-AMP can learn that the signal takes on only the values {0,1} and exploit its structure for improved reconstruction accuracy.
% Declare dimensions N = 1000; % signal length del = 0.4; % measurement-to-signal ratio, M/N rho = 0.4; % sparsity-to-measurement ratio, K/M SNR = 30; % SNR (in dB) M = ceil(del*N); %Find appropriate measurement size K = floor(rho*M); %Find appropriate sparsity if K == 0 K = 1; %Ensure at least one active coefficient. end % Generate matrix clear Params Params.M = M; Params.N = N; Params.type = 1; Params.realmat = true; Amat = generate_Amat(Params); % Generate sparse signal xtrue = zeros(N,1); % initialize signal vector xtrue(randperm(N,K)) = 1; %Bernoulli signal % Generate noisy outputs ztrue = Amat*xtrue; % compute true transform-output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output % Run, time, and check performance of EMGMAMP clear optEM optEM.heavy_tailed = false; % since operating on a sparse signal time5 = tic; [xhat,EMfin] = EMGMAMP(y, Amat, optEM); %[xhat,EMfin,estHist,~,optGAMPfin] = EMGMAMP(y, Amat, optEM); figure(3); gampShowHist(estHist,optGAMPfin,xtrue,ztrue); time5 = toc(time5) NMSE_dB5 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) % Plot the true and estimated signals figure(5) plot(xtrue,'b+'); hold on plot(xhat,'ro'); hold off xlabel('Signal Index'); ylabel('Values') title('Case 2: Bernoulli Signal, Med Sparsity, High SNR')
time5 =
0.3639
NMSE_dB5 =
-53.0791
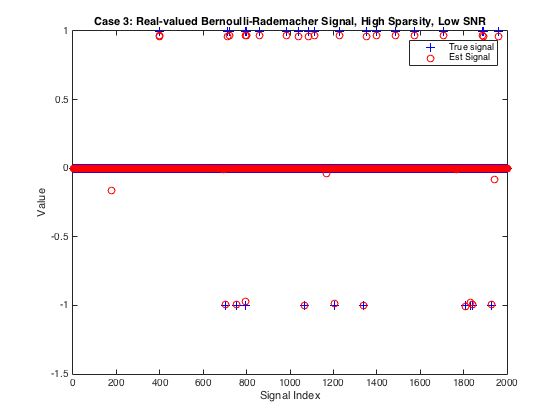
Example 3: Real Bernoulli-Rademacher Signal
Let's see if EM-GM-AMP can learn that the signal takes on only the values {0,-1,+1} and exploit its structure for improved reconstruction accuracy. This time we'll use a lower SNR.
% Declare dimensions N = 2000; % signal length del = 0.1; % measurement-to-signal ratio, M/N rho = 0.15; % sparsity-to-measurement ratio, K/M SNR = 15; % SNR (in dB) M = ceil(del*N); K = floor(rho*M); if K == 0 K = 1; %Ensure at least one active coefficient. end % Generate matrix clear Params Params.M = M; Params.N = N; Params.type = 1; Params.realmat = true; Amat = generate_Amat(Params); % Generate sparse signal xtrue = zeros(N,1); xtrue(randperm(N,K)) = sign(randn(K,1)); % Generate noisy outputs ztrue = Amat*xtrue; % compute true transform-output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output % Run, time, and check performance of EMGMAMP clear optEM optEM.heavy_tailed = false; % since operating on a sparse signal time6 = tic; xhat = EMGMAMP(y, Amat, optEM); time6 = toc(time6) NMSE_dB6 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) % Report EMGMAMP's NMSE (in dB) % Plot the true and estimated signals figure(6) plot(xtrue,'b+');hold on plot(xhat,'ro'); hold off xlabel('Signal Index'); ylabel('Value') title(sprintf('Case 3: Real-valued Bernoulli-Rademacher Signal, High Sparsity, Low SNR')) legend('True signal', 'Est Signal')
time6 =
0.8080
NMSE_dB6 =
-26.6891
Example 4: Heavy-tailed signal
Lets try EM-GM-AMP on a heavy tailed signal (non-compressible Student's T) with Infinite SNR using a Random Rademacher matrix.
% Declare dimensions N = 1000; % signal length del = 0.65; % measurement-to-signal ratio, M/N SNR = Inf; % SNR (in dB) M = ceil(del*N); % Generate matrix clear Params Params.M = M; Params.N = N; Params.realmat = true; Params.type = 2; % specify Rademacher {-1,+1} matrix Params.realmat = true; Amat = generate_Amat(Params); % Generate heavy-tailed, non-sparse signal xtrue = random('t',1.5,N,1); % Generate noisy outputs ztrue = Amat*xtrue; % compute true transform-output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output % Run, time, and check performance of EMGMAMP clear optEM optEM.heavy_tailed = true; % since operating on a heavy-tailed signal time7 = tic; xhat = EMGMAMP(y, Amat); time7 = toc(time7) NMSE_dB7 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) % Report EMGMAMP's NMSE (in dB) % Plot the true and estimated signals figure(7) plot(xtrue,'b+'); hold on plot(xhat,'ro'); hold off xlabel('Signal Index'); ylabel('Value') title(sprintf('Case 4: Students T, Inf SNR')) legend('True signal', 'Est Signal')
time7 =
1.8272
NMSE_dB7 =
-18.2786