EM-BG-AMP Algorithm: Usage Examples
Jeremy Vila and Philip Schniter, Nov. 2015
EM-BG-AMP attempts to recover a sparse signal of length N through (possibly) noisy measurements of length M (with perhaps M < N). We model this through the linear system
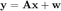 .
.
Please refer to the paper EM-BG-AMP by Jeremy Vila Philip Schniter for a detailed description of the algorithm. This manual will show how to use the EM-BG-AMP MATLAB code and how to intepret the results.
Contents
Generating Data
The following examples will use randomly generated data. First, we create the K-sparse signal, then the M-by-N measurement matrix, and finally the AWGN-corrupted measurements.
clear all close all % Check that EMGMAMP.m is on the path if exist('EMGMAMP.m')~=2 error('EMGMAMP.m not on the path') end % Choose between the new and old versions of EMGMAMP newEM = true; EMGMpath = fileparts(which('EMGMAMP')); % current path to EMGM [GAMPdir,EMGMver] = fileparts(EMGMpath); % GAMPmatlab dir and EMGM version if newEM if strcmp(EMGMver,'EMGMAMP') rmpath(EMGMpath) addpath([GAMPdir,'/EMGMAMPnew']) warning('Changing path from old to new version of EMGMAMP') end else if strcmp(EMGMver,'EMGMAMPnew') rmpath(EMGMpath) addpath([GAMPdir,'/EMGMAMP']) warning('Changing path from new to old version of EMGMAMP') end end % Declare dimensions N = 1000; % signal length del = 0.4; % measurement-to-signal ratio, M/N rho = 0.4; % sparsity-to-measurement ratio, K/M SNR = 30; % SNR (in dB) M = ceil(del*N); % measurement length K = floor(rho*M); % sparsity if K==0 K = 1; % ensure at least one active coefficient end % Generate matrix clear Params; Params.M = M; Params.N = N; Params.realmat = true; % specify real-valued matrix Params.type = 1; % specify i.i.d. Gaussian matrix Amat = generate_Amat(Params); % generate random matrix % Generate sparse signal active_mean = 1; % mean of non-zero components active_var = 1; % variance of non-zero components xtrue = zeros(N,1); % initialize signal vector xtrue(randperm(N,K)) = (sqrt(active_var)*randn(K,1)+active_mean); % Generate noisy outputs ztrue = Amat*xtrue; % compute true output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output
The Standard Way to Invoke EM-BG-AMP
Using the EM-BG-AMP algorithm is extremely easy. You simply need the measurements and measurement matrix. The algorithm returns signal estimate, the learned parameters of the assumed Bernoulli-Gaussian prior, as well as the AWGN variance.
% Run, time, and check performance of EMBGAMP optEM.heavy_tailed = false; % since operating on a sparse signal time = tic; [xhat, EMfin] = EMBGAMP(y, Amat, optEM); time = toc(time) NMSE_dB = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) wvar_error_dB = 10*log10(EMfin.noise_var/wvar) active_mean_error_dB = 10*log10(EMfin.active_mean/active_mean) active_var_error_dB = 10*log10(EMfin.active_var/active_var) sparsity_error_dB = 10*log10(EMfin.lambda/(K/N))
time =
0.4861
NMSE_dB =
-30.8079
wvar_error_dB =
0.4500
active_mean_error_dB =
0.1270
active_var_error_dB =
0.4844
sparsity_error_dB =
0.0048
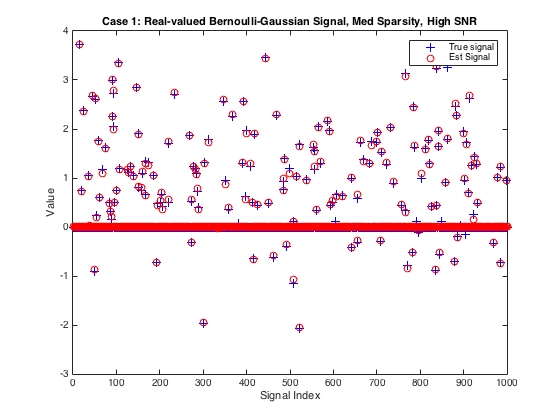
Plot the true and estimated signals
figure(2) plot(xtrue,'b+');hold on % plot true signal plot(xhat,'ro'); hold off % plot signal estimate xlabel('Signal Index'); ylabel('Value') title('Case 1: Real-valued Bernoulli-Gaussian Signal, Med Sparsity, High SNR') legend('True signal', 'Est Signal')
Exploiting Prior Signal Knowledge with EM-BG-AMP
Sometimes one has partial knowledge of the signal prior. To exploit this, we can disable the EM learning on one or more parameters.
% Set initial BG parameters at the true values clear optEM optEM.active_mean = 1; %Initialize at correct active mean optEM.active_weights = 1; %Trivial weights since 1-term mixture optEM.active_var = 1; %Initialize correct active variance optEM.noise_var = wvar; %Initialize at correct noise variance % Turn off EM learning of all but the sparsity-rate, lambda optEM.learn_lambda= true; optEM.learn_mean = false; optEM.learn_weights = false; optEM.learn_var = false; optEM.learn_noisevar = false; % Run, time, and check performance of EMBGAMP optEM.heavy_tailed = false; % since operating on a sparse signal time2 = tic; xhat = EMBGAMP(y, Amat,optEM); time2 = toc(time2) NMSE_dB2 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) sparsity_error_dB = 10*log10(EMfin.lambda/(K/N))
time2 =
0.0935
NMSE_dB2 =
-30.9412
sparsity_error_dB =
0.0048
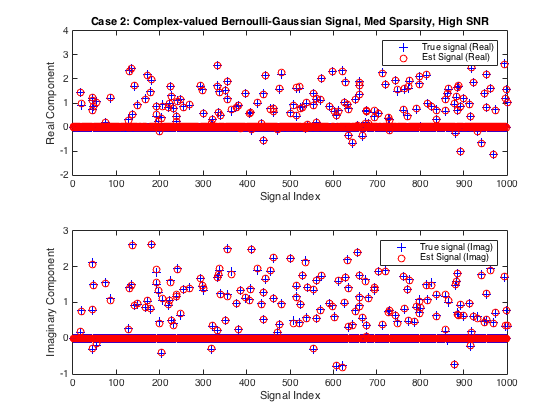
Example 2: Complex Bernoulli-Gaussian Signal
EM-BG-AMP can also handle complex-valued signals and measurements. Let's try it.
% Declare dimensions N = 1000; % signal length del = 0.4; % measurement-to-signal ratio, M/N rho = 0.4; % sparsity-to-measurement ratio, K/M SNR = 30; % SNR (in dB) M = ceil(del*N); % measurement length K = floor(rho*M); % sparsity if K==0 K = 1; % ensure at least one active coefficient end % Generate matrix clear Params; Params.M = M; Params.N = N; Params.realmat = false; % specify complex-valued matrix Params.type = 1; % specify i.i.d. Gaussian matrix Amat = generate_Amat(Params); % generate random matrix % Generate sparse signal active_mean = 1+1i; % mean of non-zero components active_var = 1; % variance of non-zero components xtrue = zeros(N,1); % initialize signal vector xtrue(randperm(N,K)) = (sqrt(active_var/2)*randn(K,2)*[1;1i]+active_mean); % Generate noisy outputs ztrue = Amat*xtrue; % compute true output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar/2)*(randn(M,2)*[1;1i]); % compute noisy output % Run, time, and check performance of EMBGAMP optEM.heavy_tailed = false; % since operating on a sparse signal time5 = tic; [xhat, EMfin] = EMBGAMP(y, Amat, optEM); time5 = toc(time5) NMSE_dB5 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) wvar_error_dB5 = 10*log10(EMfin.noise_var/wvar) % Plot the true and estimated signals figure(2) subplot(2,1,1) plot(real(xtrue),'b+'); hold on plot(real(xhat),'ro'); hold off xlabel('Signal Index'); ylabel('Real Component') title('Case 2: Complex-valued Bernoulli-Gaussian Signal, Med Sparsity, High SNR') legend('True signal (Real)', 'Est Signal (Real)') subplot(2,1,2) plot(imag(xtrue),'b+'); hold on plot(imag(xhat),'ro'); hold off xlabel('Signal Index'); ylabel('Imaginary Component') legend('True signal (Imag)', 'Est Signal (Imag)')
time5 =
0.1741
NMSE_dB5 =
-32.2383
wvar_error_dB5 =
-1.2392
Example 3: Real-valued Bernoulli-Rademacher Signal
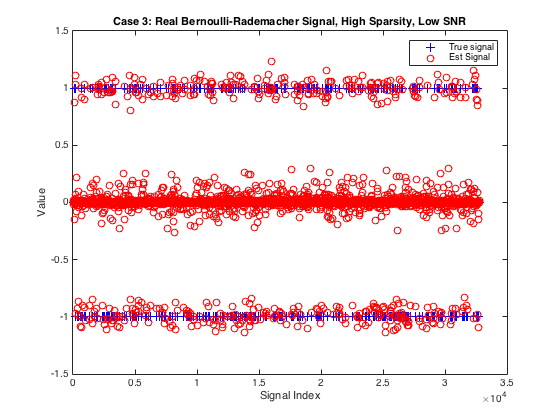
Let's see if EM-BG-AMP can learn that the signal takes on only the values {0,1} and exploit its structure for improved reconstruction accuracy. Also, let's use the oversampled DFT operator this time, meaning the measurements are complex but the signal is real-valued.
N = 2^15; % specify power-of-2 value for N del = 0.1; % measurement-to-signal ratio, M/N rho = 0.15; % sparsity-to-measurement ratio, K/M SNR = 15; % SNR (in dB) M = ceil(del*N); % measurement length K = floor(rho*M); % sparsity if K == 0 K = 1; % ensure at least one active coefficient end % Generate matrix clear Params; Params.M = M; Params.N = N; Params.realmat = true; Params.type =3; % specify a DFT operator with random row selection Amat = generate_Amat(Params); % Generate sparse signal xtrue = zeros(N,1); xtrue(randperm(N,K)) = sign(randn(K,1)); % Generate noisy outputs ztrue = Amat.mult(xtrue); % compute true output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar/2)*(randn(M,2)*[1;1i]); % compute noisy output % Run, time, and check performance of EMBGAMP optEM.heavy_tailed = false; % since operating on a sparse signal time6 = tic; [xhat, EMfin] = EMBGAMP(y, Amat, optEM); time6 = toc(time6) NMSE_dB6 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) % Report EMBGAMP's NMSE (in dB) % Plot the true and estimated signals figure(6) plot(xtrue,'b+');hold on plot(real(xhat),'ro'); hold off xlabel('Signal Index'); ylabel('Value') title(sprintf('Case 3: Real Bernoulli-Rademacher Signal, High Sparsity, Low SNR')) legend('True signal', 'Est Signal')
time6 =
4.9990
NMSE_dB6 =
-15.0711
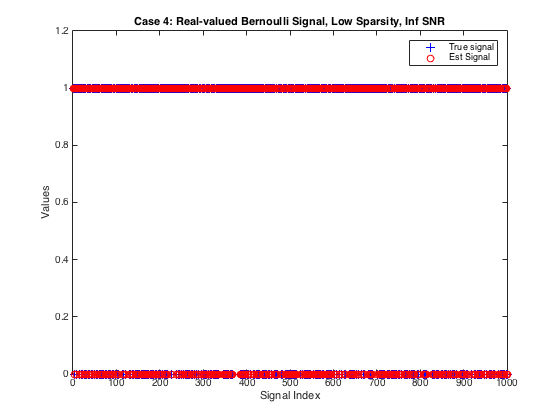
Example 4: Real-valued Bernoulli Signal
Lets try EM-BG-AMP on a Bernoulli signal with Infinite SNR and M=K (sparsity = # measurements) using a Rademacher measurement matrix. Let's also use a tighter stopping tolerance and more iterations to enable a very precise signal estimate.
N = 1000; % specify power-of-2 value for N del = 0.65; % measurement-to-signal ratio, M/N rho = 1; % sparsity-to-measurement ratio, K/M SNR = inf; % SNR (in dB) M = ceil(del*N); % measurement length K = floor(rho*M); % sparsity if K == 0 K = 1; % ensure at least one active coefficient end % Generate matrix clear Params; Params.M = M; Params.N = N; Params.realmat = true; Params.type = 2; % specify Rademacher {-1,+1} matrix Params.realmat = true; Amat = generate_Amat(Params); % Generate sparse signal xtrue = zeros(N,1); % initialize signal vector xtrue(randperm(N,K)) = 1; %Bernoulli signal % Generate noisy outputs ztrue = Amat*xtrue; % compute true transform-output vector wvar = norm(ztrue)^2/M*10^(-SNR/10); % calculate noise level y = ztrue + sqrt(wvar)*(randn(M,1)); % compute noisy output % Run, time, and check performance of EMBGAMP clear optEM optEM.heavy_tailed = false; % since operating on a sparse signal optGAMP.nit = 500; % increase the number of iterations optGAMP.tol = 1e-8; % decrease the stopping tolerance time7 = tic; xhat = EMBGAMP(y, Amat, optEM, optGAMP); time7 = toc(time7) NMSE_dB7 = 10*log10(norm(xtrue-xhat)^2/norm(xtrue)^2) %Plot signal and the estimates figure(7) plot(xtrue,'b+'); hold on plot(xhat,'ro'); hold off xlabel('Signal Index'); ylabel('Values') title(sprintf('Case 4: Real-valued Bernoulli Signal, Low Sparsity, Inf SNR')) legend('True signal', 'Est Signal')
time7 =
0.1510
NMSE_dB7 =
-165.8315