CMA-FSE ERROR SURFACE EXAMPLES
P. Bert Schniter -
Cornell University Blind Equalization Research Group
The behavior of the Constant Modulus Algorithm (CMA) as used to
adapt a Fractionally Spaced Equalizer (FSE) is illustrated
below using simple examples. Some important conclusions are then
drawn from these examples: (1) in the presence of noise or channel
undermodelling, proper initialization may be necessary to sucessfully
equalize the channel, and (2) channels containing nearly reflected
roots exhibit high levels of noise gain.
Background
In digital communications systems,
the path from source to receiver (i.e. the channel)
generally introduces dispersion
and multipath, making the received pulses difficult or impossible
to detect without a high probability of error. The use of equalization
in the receiver attempts to combat these linear distortions imposed
by the channel. As a linear equalizer filtering the received signal,
usually a transversal FIR implementation
is chosen. When sampling the received signal at the system
baud rate, we refer to the equalizer as baud spaced. When
operating at a sample rate higher than baud (a typical choice being
twice the baud rate), we refer to the equalizer as fractionally
spaced. The use of FSEs is nearly ubiquitous in recent
designs due to advantages in performance over baud spaced
equalizers. It can be shown [2] that perfect
equalization is possible with FSEs longer than the channel
delay spread for channels not exhibiting reflected
roots.
In addition to dispersion and multipath, the channel can introduce
noise. In general, the equalizer must make a compromise
between compensating for linear channel distortions and attenuating noise.
In the presence of noise, the ability to perfectly equalize is lost.
In many cases, the receiver does not know the channel characteristics
(possibly because of a newly initiated connection or because of a
rapidly varying channel). To remedy this, it may be possible to
transmit a known training signal
from which the receiver can extract the current channel characteristics.
In some situations, however, the amount of channel capacity
used by this scheme
cannot be tolerated, and the receiver must instead determine the channel
characteristics blindly. CMA is the most widely
established algorithm for accomplishing blind equalization.
Motivation
Similar to LMS, CMA can be considered a stochastic
gradient algorithm. This means that the convergence of the equalizer
parameter vector under CMA can be viewed as a (stochastic) traversal of
the CMA cost surface with average movement in the direction of
steepest descent. Thus, great insights into the dynamical behavior of
CMA can be gained from an understanding of the topology of the CMA cost
surface.
What follows are simple two-dimensional examples that help to illustrate
the salient characteristics of the CMA cost surface in the case of
fractionally spaced equalization.
Restricting the scope to two real-valued equalizer taps makes the surface
possible to visualize as a 3D object and allows us to identify important
features which also exist in the general (i.e. higher dimensional) case.
Illustrations of the CMA-FSE Cost Surface
In one regard, the goal of CMA
is to transfer a set of initial equalizer parameters to
the lowest point on the CMA cost surface. As evident below, there may
be multiple locations on the cost surface attaining the minimum cost.
As such, they represent equally desirable solutions.
All of the contour plots exhibit the following properties: at the
origin there exists a maximum, surrounded by a ring of up to
four minima. Minima reflected across the origin correspond to
solutions differing only in sign, which is inconsequential when
using differential coding. Finally, as we travel further from the
origin, the surface rises steeply in all directions.
It should be noted that, though the following surfaces were created from
particular channels,
they are intended to be prototypical of their
respective channel classes. For simplicity, BPSK was chosen as the
model for the source statistics, though the thrust of the conclusions
below applies to higher-order constellations (e.g. 64-QAM) as well.
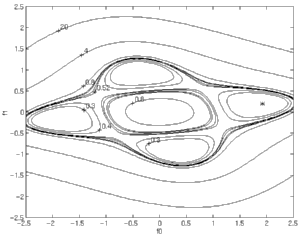
|
Perfect Equalizability with Well-Behaved Channel
In the case of perfect equalizability, all four minima correspond to
the same (optimal) CMA cost of zero. Each minima reflects a
particular combination of system delay and system polarity. The
asterisk indicates the location of a particular Wiener solution.
Since there is no noise, it appears coincident with the CMA cost
minimum of corresponding system delay and polarity. |
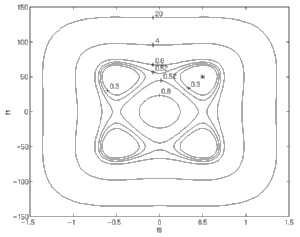
|
Perfect Equalizability with Nearly-Reflected Channel Roots
As channel roots become more nearly reflected, the surface becomes
more elongated.
Note the scaling on the vertical axis is 100 times that on the
horizontal axis! This characteristic will be
manifested as an extremely slow convergence of the 'f1' equalizer tap
due to the shallowness of the gradient along that dimension.
Theoretically, however, perfect equalizability is still
possible in the noiseless case. In other words, all minima correspond
to zero cost and are aligned with the respective Wiener solutions. |
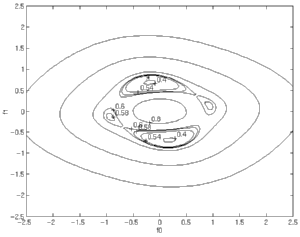
|
Noisy but Well-Behaved Channel
When the well-behaved channel (i.e. the first plot above) is operated
in a 7dB SNR environment,
note the appearance of local minima distinct from the global
minima. For particular initializations, local minima are capable
of capturing the parameter
trajectory and preventing it from attaining an optimum setting.
Note that all minima correspond to costs greater than zero since perfect
equalization is not possible in the presence of noise. |
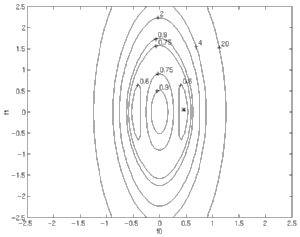
|
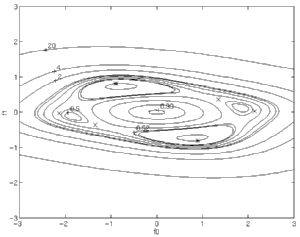
Noisy Channel with Nearly-Reflected Roots
When the channel with nearly reflected roots (above) is operated in a 7dB
SNR environment, we see a dramatic change in the cost surface.
Note the equivalent scaling of horizontal and vertical axes; the cost surface
has become much less elongated than in the noiseless case (see the second
picture in the series).
Also note the merging of two pairs of
minima into one pair. For this channel, the optimal solution in the
presence of noise is very different from the solution which perfectly
equalizes the channel. |
|
Undermodelled but Well-Behaved Channel, No Noise
When the delay spread of the channel is longer than the delay
spread of the FSE, we lose the ability to perfectly equalize. Thus,
none of the minima correspond to zero cost. More importantly, note the
existence of local minima with greater CMA cost than the global minima.
This implies that the equalizer initialization will determine the
optimality of the resulting CMA solution. |
Conclusions
The examples above emphasize a few facts. First, the FSE-CMA cost surface
is multimodal, by virtue of the existence of multiple minima. In the
case where an FSE is able to perfectly equalize the channel, all minima
correspond to the same optimal CMA cost. Furthermore, it can
be shown that these multiple minima occur very near to the Wiener solutions
corresponding to particular combinations of system polarity and system
delay [3]. By system delay, we mean the delay through the cascaded channel
and equalizer. By sytem polarity, we mean {+,-} in the case of real
signals or {+,-,+j,-j} in the case of complex signals.
Next, channels with nearly-reflected roots will most likely exhibit
very slow FSE parameter convergence rates in the absence of noise. Adding the
effects of noise, the FSE may not even come close to equalizing the channel.
Well behaved channels are not as sensitive to noise as those
with nearly reflected roots.
Any time noise is present, though,
we can expect local minima. This implies the potential for
convergence to non-optimal CMA solutions and places importance on
the choice of initialization. The same holds true for FSEs that
undermodel the channel, even for well-behaved channels in the absence
of noise. Initialization can be extremely important if, in these cases,
there exist bad local minima which do not correspond to open
eye solutions. By open eye, we mean that the channel has been
equalized enough to successfully transfer adaptation to a decision-
directed equalization scheme. If CMA converges to one of these
bad local minima, there is little chance of successfully demodulating the
incoming data. In such cases, the system must be restarted, possibly with
a different initialization, in the hope that CMA will converge to an
open-eye solution.
Questions for Practitioners
The examples presented in this demonstration help to motivate the
search for techniques that avoid the problems associated with CMA's
sensitivity to poor choices of initialization. In practice, it is
typical to use a center-spike initialization, whereby the center
equalizer tap is made unity and all other taps are made zero.
Though originally suggested in [1], we know of no theoretical work
that has rigorously defended this technique.
The question remains as to how well the center-spike initialization
really works. We have received reports of the center-spike method
failing on occasion, but have not received any specific examples.
Can anyone provide us with some?
References
[1] D.N. Godard, "Self-Recovering Equalization and Carrier Tracking in
Two-Dimensional Data Communication Systems," IEEE Trans. Commun.,
Vol. COM-28, No.11, Nov. 1980.
[2] J.R. Treichler, I. Fijalkow, and C.R. Johnson, Jr., "Fractionally
Spaced Equalizers - How long should they really be?," Signal
Processing, pp.65-81, May 1996.
[3] H.H. Zeng, L. Tong, and C.R. Johnson, Jr., "Relationships Between
CMA and Wiener Receivers," Submitted to IEEE Trans. on Inform.
Theory.
Further Reading
The examples and discussion above are drawn from a
technical report written by members of Cornell's
Blind Equalization Research Group (BERG). The report includes
a derivation of the equations respresenting CMA-FSE cost with arbitrary
source kurtosis (i.e. for any constellation) and in the presence
of additive white gaussian channel noise.
Matlab Code
The
BERGulator can be used to generate these surfaces and others.




