Contents
function results = trial_rpca(optIn)
setup_RPCA
if nargin == 0
clc
defaultStream = RandStream.getGlobalStream;
if 1
savedState = defaultStream.State;
save random_state.mat savedState;
else
load random_state.mat
end
defaultStream.State = savedState;
optIn.tryBigamp = 1;
optIn.tryBigampEM = 1;
optIn.tryBigampEMcontract = 1;
optIn.tryGrasta = 1;
optIn.tryInexactAlm = 1;
optIn.tryVbrpca = 1;
optIn.tryLmafit = 1;
optIn.M = 200;
optIn.L = 200;
optIn.N = 10;
optIn.p1 = 1;
optIn.lambda = 0.25;
optIn.nuw = [0 20^2/12];
end
Problem Setup
tryBigamp = optIn.tryBigamp;
tryBigampEM = optIn.tryBigampEM;
tryBigampEMcontract = optIn.tryBigampEMcontract;
tryGrasta = optIn.tryGrasta;
tryInexactAlm = optIn.tryInexactAlm;
tryVbrpca = optIn.tryVbrpca;
tryLmafit = optIn.tryLmafit;
if isfield(optIn,'lambda_inexactAlm')
lambda_inexactAlm = optIn.lambda_inexactAlm;
else
lambda_inexactAlm = 1/sqrt(optIn.M);
end
nuw = optIn.nuw;
lambda = optIn.lambda;
M = optIn.M;
L = optIn.L;
N = optIn.N;
p1 = optIn.p1;
opt = BiGAMPOpt;
problem = BiGAMPProblem();
problem.M = M;
problem.N = N;
problem.L = L;
Build true low rank matrix
X = randn(N,L);
A = randn(M,N);
Z = A*X;
Form the output channel
inds = rand(size(Z)) < lambda;
errorWidth = sqrt(12*nuw(2));
Y = Z +...
sqrt(nuw(1))*randn(size(Z)) +...
(-errorWidth/2 + errorWidth*rand(size(Z))).*inds;
X2 = zeros(size(Y));
X2(inds) = Y(inds) - Z(inds);
omega = false(M,L);
ind = randperm(M*L);
omega(ind(1:ceil(p1*M*L))) = true;
Y(~omega) = 0;
if p1 < 1
[problem.rowLocations,problem.columnLocations] = find(omega);
end
error_function = @(qval) 20*log10(norm(qval - Z,'fro') / norm(Z,'fro'));
opt.error_function = error_function;
Establish the channel objects
gX = AwgnEstimIn(zeros(size(X)), ones(size(X)));
gA = AwgnEstimIn(zeros(size(A)), ones(size(A)));
gOutBase = GaussMixEstimOut(Y,nuw(1),nuw(2),lambda);
gOut = MaskedEstimOut(gOutBase,omega);
Control initialization
opt.xhat0 = zeros(N,L);
opt.Ahat0 = randn(M,N);
opt.Avar0 = 10*ones(M,N);
opt.xvar0 = 10*ones(N,L);
results = [];
Switch to Non-adaptive
opt.stepMin = 0.25;
opt.stepMax = 0.25;
opt.adaptStep = 0;
Run BiGAMP-1
if tryBigamp
failCounter = 0;
tryAgain = 1;
failTime = 0;
while tryAgain
failCounter = failCounter + 1;
disp('Starting BiG-AMP-1')
tstart = tic;
[estFin,~,estHist] = ...
BiGAMP(gX, gA, gOut, problem, opt);
tGAMP = toc(tstart);
[~,~,p1] = gOutBase.estim(estFin.Ahat*estFin.xhat,estFin.pvar);
if max(sum(p1)) > 0.8*M || max(sum(p1.')) > 0.8*L
disp('Misconverged, trying again...')
tryAgain = true;
opt.Ahat0 = randn(size(opt.Ahat0));
failTime = failTime + estHist.timing(end);
else
tryAgain = false;
end
if failCounter >= 5
tryAgain = false;
end
end
estHist.timing = estHist.timing + failTime;
loc = length(results) + 1;
results{loc}.name = 'BiG-AMP-1';
results{loc}.err = estHist.errZ(end);
results{loc}.time = tGAMP;
results{loc}.errHist = estHist.errZ;
results{loc}.timeHist = estHist.timing;
end
Starting BiG-AMP-1
Switch to adaptive
opt.stepMin = 0.05;
opt.stepMax = 0.5;
opt.adaptStep = 1;
Specify Q
Q = orth(randn(M));
error_functionQ = @(qval) 20*log10(norm(Q'*qval - Z,'fro') / norm(Z,'fro'));
opt.error_function = error_functionQ;
Run alternative BiGAMP
gOut2 = AwgnEstimOut(Q*Y,nuw(1));
A2 = MatrixLinTrans(Q);
lambdaMatrix = lambda*ones(M,L);
lambdaMatrix(~omega) = 1;
inputEst = AwgnEstimIn(0, nuw(2));
gX2 = SparseScaEstim(inputEst,lambdaMatrix);
opt.error_functionX2 =...
@(q) 20*log10(norm(q(omega) - X2(omega),'fro')/norm(X2(omega),'fro'));
opt.x2hat0 = zeros(M,L);
opt.x2var0 = 10*lambda*nuw(2)*ones(M,L);
opt.xhat0 = zeros(N,L);
opt.xvar0 = 10*ones(N,L);
opt.Avar0 = 10*ones(M,N);
if tryBigamp
failCounter = 0;
tryAgain = 1;
failTime = 0;
while tryAgain
failCounter = failCounter + 1;
disp('Starting BiG-AMP-2')
tstart = tic;
[estFin2,~,estHist2] = ...
BiGAMP_X2(gX, gA, gX2, A2, gOut2, problem, opt);
tGAMP2 = toc(tstart);
[~,~,~,p1] = gX2.estim(estFin2.r2hat,estFin2.r2var);
if max(sum(p1)) > 0.8*M || max(sum(p1.')) > 0.8*L
disp('Misconverged, trying again...')
tryAgain = true;
opt.Ahat0 = randn(size(opt.Ahat0));
failTime = failTime + estHist2.timing(end);
else
tryAgain = false;
end
if failCounter >= 5
tryAgain = false;
end
end
estHist2.timing = estHist2.timing + failTime;
loc = length(results) + 1;
results{loc}.name = 'BiG-AMP-2';
results{loc}.err = estHist2.errZ(end);
results{loc}.time = tGAMP2;
results{loc}.errHist = estHist2.errZ;
results{loc}.timeHist = estHist2.timing;
end
Warning: Tiny non-zero variances will be used for computing log likelihoods. May
cause problems with adaptive step size if used.
Starting BiG-AMP-2
EM BiG AMP
if tryBigampEM
opt.verbose = false;
disp('Starting EM-BiG-AMP-2')
tstart = tic;
[estFinEM,~,~,estHistEM] = ...
EMBiGAMP_RPCA(Y,A2,problem,opt);
tEMGAMP = toc(tstart);
loc = length(results) + 1;
results{loc}.name = 'EM-BiG-AMP-2';
results{loc}.err = estHistEM.errZ(end);
results{loc}.time = tEMGAMP;
results{loc}.errHist = estHistEM.errZ;
results{loc}.timeHist = estHistEM.timing;
end
Starting EM-BiG-AMP-2
It 0001 nuX = 1.786e-01 nuX2 = 3.497e+01 Lam = 0.10 tol = 1.000e-04 SNR = 20.00 Z_e = -49.3132 X2_e = -40.9036 numIt = 0048
It 0002 nuX = 2.794e-01 nuX2 = 3.465e+01 Lam = 0.24 tol = 3.051e-05 SNR = 45.16 Z_e = -70.2827 X2_e = -62.1218 numIt = 0030
It 0003 nuX = 2.795e-01 nuX2 = 3.334e+01 Lam = 0.25 tol = 2.278e-07 SNR = 66.42 Z_e = -97.0103 X2_e = -88.9233 numIt = 0039
It 0004 nuX = 2.795e-01 nuX2 = 3.318e+01 Lam = 0.25 tol = 1.000e-08 SNR = 93.27 Z_e = -146.7006 X2_e = -146.0320 numIt = 0037
It 0005 nuX = 2.795e-01 nuX2 = 3.315e+01 Lam = 0.25 tol = 1.000e-08 SNR = 151.05 Z_e = -158.3186 X2_e = -157.6460 numIt = 0030
EM BiG AMP with rank contraction
if tryBigampEMcontract
opt.verbose = false;
EMopt.learnRank = true;
EMopt.rankMax = 90;
disp('Starting EM-BiG-AMP-2 with rank contraction')
tstart = tic;
[estFinEM,~,~,estHistEM] = ...
EMBiGAMP_RPCA(Y,A2,problem,opt,EMopt);
tEMGAMP = toc(tstart);
loc = length(results) + 1;
results{loc}.name = 'EM-BiG-AMP-2 (Rank Contraction)';
results{loc}.err = estHistEM.errZ(end);
results{loc}.time = tEMGAMP;
results{loc}.errHist = estHistEM.errZ;
results{loc}.timeHist = estHistEM.timing;
results{loc}.rank = size(estFin.xhat,1);
end
Starting EM-BiG-AMP-2 with rank contraction
It 0001 nuX = 1.984e-02 nuX2 = 3.497e+01 Lam = 0.10 tol = 1.000e-04 SNR = 20.00 Z_e = -23.8473 X2_e = -20.4914 numIt = 0050
Updating rank estimate from 90 to 10 on iteration 1
It 0002 nuX = 2.154e-02 nuX2 = 4.515e+01 Lam = 0.20 tol = 1.000e-04 SNR = 24.44 Z_e = -42.2848 X2_e = -34.7173 numIt = 0052
It 0003 nuX = 1.355e-01 nuX2 = 3.485e+01 Lam = 0.24 tol = 1.000e-04 SNR = 38.89 Z_e = -61.7464 X2_e = -53.4662 numIt = 0030
It 0004 nuX = 1.362e-01 nuX2 = 3.351e+01 Lam = 0.25 tol = 1.682e-06 SNR = 57.74 Z_e = -89.6134 X2_e = -81.2595 numIt = 0035
It 0005 nuX = 1.362e-01 nuX2 = 3.320e+01 Lam = 0.25 tol = 1.000e-08 SNR = 85.54 Z_e = -147.0404 X2_e = -146.3593 numIt = 0043
It 0006 nuX = 1.362e-01 nuX2 = 3.315e+01 Lam = 0.25 tol = 1.000e-08 SNR = 151.82 Z_e = -161.3852 X2_e = -160.7517 numIt = 0030
Try LMaFit
if tryLmafit
disp('Starting LMaFit')
Lmafit_opts.tol = opt.tol;
Lmafit_opts.maxit = 6000;
Lmafit_opts.est_rank = 0;
tstart = tic;
[Almafit,Xlmafit,~,~,timingLmafit,estHistLmafit] = lmafit_sms_v1_timing(Y,N,Lmafit_opts,[],error_function);
tLmafit = toc(tstart);
ZhatLMaFit = Almafit*Xlmafit;
errLMaFit = 20*log10(norm(ZhatLMaFit(:) - Z(:)) / norm(Z(:)));
loc = length(results) + 1;
results{loc}.name = 'LMaFit';
results{loc}.err = errLMaFit;
results{loc}.time = tLmafit;
results{loc}.errHist = estHistLmafit.errZ;
results{loc}.timeHist = timingLmafit;
end
Starting LMaFit
Try GRASTA
if tryGrasta
disp('Starting GRASTA')
maxCycles = 20;
OPTIONS.QUIET = opt.verbose;
OPTIONS.MAX_LEVEL = 20;
OPTIONS.MAX_MU = 15;
OPTIONS.MIN_MU = 1;
OPTIONS.DIM_M = M;
OPTIONS.RANK = N;
OPTIONS.ITER_MIN = 20;
OPTIONS.ITER_MAX = 20;
OPTIONS.rho = 2;
OPTIONS.TOL = 1e-8;
OPTIONS.stopTol = opt.tol;
OPTIONS.USE_MEX = 0;
CONVERGE_LEVEL = 20;
[I,J] = find(omega);
S = reshape(Y(omega),[],1);
tstart = tic;
[Usg, Vsg, ~,timingGrasta,estHistGrasta] =...
grasta_mc_timing(I,J,S,M,L,maxCycles,CONVERGE_LEVEL,OPTIONS,error_function);
tGrasta = toc(tstart);
ZhatGrasta = Usg*Vsg';
errGrasta = 20*log10(norm(ZhatGrasta(:) - Z(:)) / norm(Z(:)));
loc = length(results) + 1;
results{loc}.name = 'GRASTA';
results{loc}.err = errGrasta;
results{loc}.time = tGrasta;
results{loc}.errHist = estHistGrasta.errZ;
results{loc}.timeHist = timingGrasta;
end
Starting GRASTA
Level 0: 1.15e-02
multi-level adaption - increasing, t:4.98e-01, vectors: 152, level: 1
Will use 20 ADMM iterations in level 1
multi-level adaption - increasing, t:1.77e-01, vectors: 64, level: 2
Will use 20 ADMM iterations in level 2
multi-level adaption - increasing, t:1.09e-01, vectors: 71, level: 3
Will use 20 ADMM iterations in level 3
multi-level adaption - increasing, t:6.25e-02, vectors: 74, level: 4
Will use 20 ADMM iterations in level 4
multi-level adaption - increasing, t:2.70e-02, vectors: 79, level: 5
Will use 20 ADMM iterations in level 5
multi-level adaption - increasing, t:1.14e-02, vectors: 74, level: 6
Will use 20 ADMM iterations in level 6
multi-level adaption - increasing, t:7.73e-03, vectors: 71, level: 7
Will use 20 ADMM iterations in level 7
multi-level adaption - increasing, t:3.91e-03, vectors: 91, level: 8
Will use 20 ADMM iterations in level 8
multi-level adaption - increasing, t:2.03e-03, vectors: 66, level: 9
Will use 20 ADMM iterations in level 9
multi-level adaption - increasing, t:6.13e-04, vectors: 68, level: 10
Will use 20 ADMM iterations in level 10
multi-level adaption - increasing, t:3.85e-04, vectors: 91, level: 11
Will use 20 ADMM iterations in level 11
multi-level adaption - increasing, t:2.27e-04, vectors: 99, level: 12
Will use 20 ADMM iterations in level 12
multi-level adaption - increasing, t:9.25e-05, vectors: 85, level: 13
Will use 20 ADMM iterations in level 13
multi-level adaption - increasing, t:4.94e-05, vectors: 89, level: 14
Will use 20 ADMM iterations in level 14
multi-level adaption - increasing, t:2.32e-05, vectors: 64, level: 15
Will use 20 ADMM iterations in level 15
multi-level adaption - increasing, t:7.20e-06, vectors: 84, level: 16
Will use 20 ADMM iterations in level 16
multi-level adaption - increasing, t:1.94e-06, vectors: 104, level: 17
Will use 20 ADMM iterations in level 17
multi-level adaption - increasing, t:3.51e-06, vectors: 153, level: 18
Will use 20 ADMM iterations in level 18
multi-level adaption - increasing, t:1.15e-06, vectors: 227, level: 19
Will use 20 ADMM iterations in level 19
multi-level adaption - increasing, t:5.70e-07, vectors: 398, level: 20
Will use 20 ADMM iterations in level 20
Inexact Alm
if tryInexactAlm
magicLam = sqrt(1/M);
[magicError,magicLoc] = min(abs(magicLam - lambda_inexactAlm));
if magicError < 1e-3*magicLam
magicFlag = 1;
else
magicFlag = 0;
end
for counter = 1:length(lambda_inexactAlm)
display('Starting Inexact ALM')
tstart = tic;
[~,~,~,timingInexactAlm,estHistInexactAlm] =...
inexact_alm_rpca_tasos_timing(...
Y, lambda_inexactAlm(counter), opt.tol, 200,N,error_function);
tInexactAlm = toc(tstart);
errInexactAlm = estHistInexactAlm.errZ(end);
inexactAlmResults{counter}.errInexactAlm = errInexactAlm;
inexactAlmResults{counter}.tInexactAlm = tInexactAlm;
inexactAlmResults{counter}.errInexactAlmHist = estHistInexactAlm.errZ;
inexactAlmResults{counter}.tInexactAlmHist = timingInexactAlm;
end
myfun = @(q) q.errInexactAlm;
yada = cellfun(myfun,inexactAlmResults);
[~,best_lambda] = min(yada);
if magicFlag
loc = length(results) + 1;
results{loc}.name = 'IALM-1';
results{loc}.err = inexactAlmResults{magicLoc}.errInexactAlm;
results{loc}.time = inexactAlmResults{magicLoc}.tInexactAlm;
results{loc}.errHist = inexactAlmResults{magicLoc}.errInexactAlmHist;
results{loc}.timeHist = inexactAlmResults{magicLoc}.tInexactAlmHist;
end
finalTimes = cellfun(@(q) q.tInexactAlmHist(end),inexactAlmResults);
loc = length(results) + 1;
results{loc}.name = 'IALM-2';
results{loc}.err = inexactAlmResults{best_lambda}.errInexactAlm;
results{loc}.time = sum(cellfun(@(q) q.tInexactAlm,inexactAlmResults));
results{loc}.errHist = inexactAlmResults{best_lambda}.errInexactAlmHist;
results{loc}.timeHist = inexactAlmResults{best_lambda}.tInexactAlmHist...
+ sum(finalTimes) - finalTimes(best_lambda);
end
Starting Inexact ALM
Try VBRPCA
if tryVbrpca
options.thr = opt.tol;
options.verbose = opt.verbose;
options.initial_rank = N;
options.DIMRED = 0;
options.inf_flag = 2;
options.MAXITER = 300;
options.UPDATE_BETA = 1;
options.mode = 'VB';
disp('Starting VBRPCA');
tstart = tic;
[timingVbrpca,estHistVbrpca,Zvbrpca,~,~,X2vbrpca] =...
VBRPCA_timing(Y, options,error_function);
tVbrpca = toc(tstart);
if opt.verbose
X1_error_vbrpca = error_function(Zvbrpca)
X2_error_vbrpca = opt.error_functionX2(X2vbrpca)
end
loc = length(results) + 1;
results{loc}.name = 'VSBL';
results{loc}.err = estHistVbrpca.errZ(end);
results{loc}.time = tVbrpca;
results{loc}.errHist = estHistVbrpca.errZ;
results{loc}.timeHist = timingVbrpca;
end
Starting VBRPCA
Store the options structures in results
results{1}.optIn = optIn;
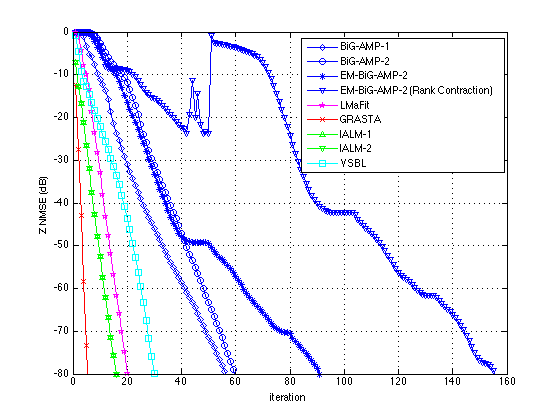
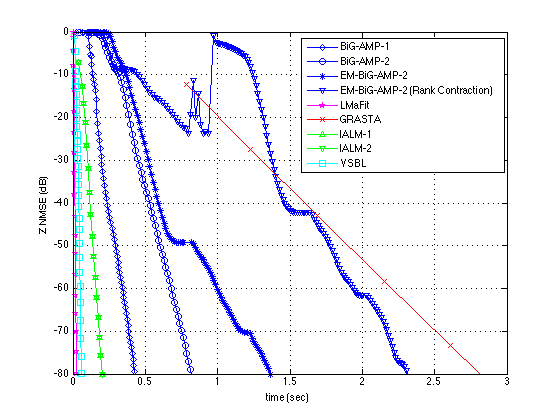
Show Results
if nargin == 0
plotUtilityNew(results,[-80 0],200,201)
results{:}
end
ans =
name: 'BiG-AMP-1'
err: -153.8604
time: 0.9514
errHist: [99x1 double]
timeHist: [99x1 double]
optIn: [1x1 struct]
ans =
name: 'BiG-AMP-2'
err: -149.5118
time: 1.7707
errHist: [96x1 double]
timeHist: [96x1 double]
ans =
name: 'EM-BiG-AMP-2'
err: -158.3186
time: 3.4914
errHist: [184x1 double]
timeHist: [184x1 double]
ans =
name: 'EM-BiG-AMP-2 (Rank Contraction)'
err: -161.3852
time: 4.5046
errHist: [240x1 double]
timeHist: [240x1 double]
rank: 10
ans =
name: 'LMaFit'
err: -164.3741
time: 0.0994
errHist: [40x1 double]
timeHist: [40x1 double]
ans =
name: 'GRASTA'
err: -111.4710
time: 10.1036
errHist: [12x1 double]
timeHist: [12x1 double]
ans =
name: 'IALM-1'
err: -165.0301
time: 0.6566
errHist: [36x1 double]
timeHist: [36x1 double]
ans =
name: 'IALM-2'
err: -165.0301
time: 0.6566
errHist: [36x1 double]
timeHist: [36x1 double]
ans =
name: 'VSBL'
err: -93.6951
time: 0.2000
errHist: [1x48 double]
timeHist: [1x48 double]
ans =
Columns 1 through 4
[1x1 struct] [1x1 struct] [1x1 struct] [1x1 struct]
Columns 5 through 8
[1x1 struct] [1x1 struct] [1x1 struct] [1x1 struct]
Column 9
[1x1 struct]