Contents

function results = trial_matrixCompletion(optIn)

%trial_matrixCompletion: This function runs several algorithms on a sample
%instance of the matrix completion problem. The function can be run with no
%arguments. See the nargin==0 block below for the required fields to call
%the function with optional paramters. The function returns a structure of
%algorithm results.
%This code can be used to produce the results for the noise free phase
%plane plots for matrix completion in the BiG-AMP arXiv submission.
%(This code conducts a single trial at 1 point in the phase plane.)

%Add needed paths for MC examples
setup_MC

%Test case
if nargin == 0

    %Clear screen
    clc

    %Handle random seed
    defaultStream = RandStream.getGlobalStream;
    if 1 %change to zero to try the same random draw repeatedly
        savedState = defaultStream.State;
        save random_state.mat savedState;
    else
        load random_state.mat %#ok<UNRCH>
    end
    defaultStream.State = savedState;

    %Flags to test BiG-AMP variants
    optIn.tryBigampFastApproximated3 = 1; %Try BiG-AMP Lite
    optIn.tryBigamp = 1;
    optIn.tryBigampEM = 1;
    optIn.tryBigampEMcontract = 1;

    %Flags to turn on comparison algorithms
    optIn.tryInexactAlm = 1;
    optIn.tryGrouse = 1;
    optIn.tryLmafit = 1;
    optIn.tryVbmc = 1;
    optIn.tryMatrixAlps = 1;

    %Problem parameters
    optIn.SNR = inf; %Signal to Noise Ratio in dB (set to inf for noise free)
    optIn.M = 500; %Data matrix is M x L
    optIn.L = 500; %L >= M for some codes (doesn't matter for BiG-AMP)
    optIn.N = 10; %The rank
    optIn.p1 = 0.1; %fraction of observed entries


end

Problem Setup

%Flags to control BiG-AMP variants
tryBigamp = optIn.tryBigamp;
tryBigampFastApproximated3 = optIn.tryBigampFastApproximated3;
tryBigampEM = optIn.tryBigampEM;
tryBigampEMcontract = optIn.tryBigampEMcontract;

%Flags to control other algorithms
tryLmafit = optIn.tryLmafit;
tryInexactAlm  = optIn.tryInexactAlm;
tryGrouse = optIn.tryGrouse;
tryVbmc = optIn.tryVbmc;
tryMatrixAlps = optIn.tryMatrixAlps;

%Specify SNR
SNR = optIn.SNR;

%Define the true matrix size (Z and Y are MxL)
M = optIn.M;
L = optIn.L;

%Specify N, which is the rank of Z in this setup
N = optIn.N;

%Specify the fraction of on entries in Y, which we shall dub p1
p1 = optIn.p1;

%Check condition
checkVal = (M + L).*N ./ (p1 .* M .* L);
disp(['Check condition was ' num2str(checkVal)])
rho = N*(L + M - N) / p1 / M / L;
disp(['Rho was ' num2str(rho)])

Check condition was 0.4
Rho was 0.396

Define options

%Set options
opt = BiGAMPOpt; %initialize the options object

%Use sparse mode for low sampling rates
if p1 <= 0.2
    opt.sparseMode = 1;
end

Build the true low rank matrix

%Compute true input vector
X = randn(N,L);


%Build true A
A = randn(M,N);

%Noise free signal
Z = A*X;

Form the (possibly noisy) output channel

%Define the error function for computing normalized mean square error
error_function = @(qval) 20*log10(norm(qval - Z,'fro') / norm(Z,'fro'));
opt.error_function = error_function;

%Determine nuw
nuw = norm(reshape(Z,[],1))^2/M/L*10^(-SNR/10);

%Noisy output channel
Y = Z + sqrt(nuw)*randn(size(Z));

%Censor Y
omega = false(M,L);
ind = randperm(M*L);
omega(ind(1:ceil(p1*M*L))) = true;
Y(~omega) = 0;

%Specify the problem setup for BiG-AMP, including the matrix dimensions and
%sampling locations. Notice that the rank N can be learned by the EM code
%and does not need to be provided in that case. We set it here for use by
%the low-level codes which assume a known rank
problem = BiGAMPProblem();
problem.M = M;
problem.N = N;
problem.L = L;
[problem.rowLocations,problem.columnLocations] = find(omega);

Establish the channel objects for BiG-AMP

%Prior on X
gX = AwgnEstimIn(0, 1);

%Prior on A
gA = AwgnEstimIn(0, 1);


%Output log likelihood
if opt.sparseMode
    gOut = AwgnEstimOut(reshape(Y(omega),1,[]), nuw);
else
    gOut = AwgnEstimOut(Y, nuw);
end

Warning: Tiny non-zero variances will be used for computing log likelihoods. May
cause problems with adaptive step size if used. 

Control initialization

%Random initializations
Ahat = randn(M,N);
xhat = randn(N,L);


%Use the initial values
opt.xhat0 = xhat;
opt.Ahat0 = Ahat;
opt.Avar0 = 10*ones(M,N);
opt.xvar0 = 10*ones(N,L);


%Initialize results as empty
results = [];

Try BiG-AMP Lite

if tryBigampFastApproximated3

    disp('Starting BiG-AMP Lite')
    tstart = tic;
    [~,~,estHist5] = ...
        BiGAMP_Lite(Y,1,1,nuw,problem,opt);
    tGAMP5 = toc(tstart);


    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'BiG-AMP Lite';
    results{loc}.err = estHist5.errZ(end);
    results{loc}.time = tGAMP5;
    results{loc}.errHist = estHist5.errZ;
    results{loc}.timeHist = estHist5.timing;

end

Starting BiG-AMP Lite

Try BiGAMP

if tryBigamp

    disp('Starting BiG-AMP')
    %Run BGAMP
    tstart = tic;
    [estFin,~,estHist] = ...
        BiGAMP(gX, gA, gOut, problem, opt); %#ok<ASGLU>
    tGAMP = toc(tstart);



    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'BiG-AMP'; %#ok<*AGROW>
    results{loc}.err = estHist.errZ(end);
    results{loc}.time = tGAMP;
    results{loc}.errHist = estHist.errZ;
    results{loc}.timeHist = estHist.timing;


end

Starting BiG-AMP

Try EM-BiGAMP

if tryBigampEM

    disp('Starting EM-BiG-AMP')
    %Run BGAMP
    tstart = tic;
    [estFin,~,~,estHistEM] = ...
        EMBiGAMP_MC(Y,problem,opt);
    tGAMP = toc(tstart);



    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'EM-BiG-AMP'; %#ok<*AGROW>
    results{loc}.err = opt.error_function(estFin.Ahat*estFin.xhat);
    results{loc}.time = tGAMP;
    results{loc}.errHist = estHistEM.errZ;
    results{loc}.timeHist = estHistEM.timing;


end

Starting EM-BiG-AMP
It 0001 nuX = 9.906e-01 meanX = 0.000e+00 tol = 1.000e-04 nuw = 9.906e-02 SNR = 20.00 Error = -40.7539 numIt = 0052
It 0002 nuX = 8.911e-01 meanX = 0.000e+00 tol = 2.737e-05 nuw = 2.717e-04 SNR = 45.63 Error = -73.9313 numIt = 0031
It 0003 nuX = 8.941e-01 meanX = 0.000e+00 tol = 1.000e-08 nuw = 7.555e-08 SNR = 81.22 Error = -141.0238 numIt = 0055
It 0004 nuX = 8.940e-01 meanX = 0.000e+00 tol = 1.000e-08 nuw = 3.268e-08 SNR = 149.18 Error = -152.8152 numIt = 0030

Try EM-BiGAMP with rank contraction

%This version attempts to learn the matrix rank


if tryBigampEMcontract

    %Enable rank learning with rank contraction
    EMopt.learnRank = 2;

    %Limit iterations for each EM iteration
    opt.nit = 300;

    disp('Starting EM-BiG-AMP with rank contraction')
    %Run BGAMP
    tstart = tic;
    [estFin,~,~,estHistEM] = ...
        EMBiGAMP_MC(Y,problem,opt,EMopt);
    tGAMP = toc(tstart);



    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'EM-BiG-AMP (Rank Contraction)'; %#ok<*AGROW>
    results{loc}.err = opt.error_function(estFin.Ahat*estFin.xhat);
    results{loc}.time = tGAMP;
    results{loc}.errHist = estHistEM.errZ;
    results{loc}.timeHist = estHistEM.timing;
    results{loc}.rank = size(estFin.xhat,1);

end

Starting EM-BiG-AMP with rank contraction
It 0001 nuX = 3.962e-01 meanX = 0.000e+00 tol = 1.000e-04 nuw = 9.906e-02 SNR = 20.00 Error = -16.0272 numIt = 0050
Updating rank estimate from 25 to 10 on iteration 1
It 0002 nuX = 3.458e-01 meanX = 0.000e+00 tol = 1.000e-04 nuw = 9.715e-02 SNR = 19.39 Error = -38.1882 numIt = 0045
It 0003 nuX = 5.983e-01 meanX = 0.000e+00 tol = 4.811e-05 nuw = 4.763e-04 SNR = 43.18 Error = -69.8033 numIt = 0030
It 0004 nuX = 6.026e-01 meanX = 0.000e+00 tol = 2.016e-08 nuw = 2.017e-07 SNR = 76.95 Error = -135.1314 numIt = 0053
It 0005 nuX = 6.026e-01 meanX = 0.000e+00 tol = 1.000e-08 nuw = 5.181e-14 SNR = 142.86 Error = -160.3864 numIt = 0030
It 0006 nuX = 6.026e-01 meanX = 0.000e+00 tol = 1.000e-08 nuw = 5.197e-14 SNR = 168.11 Error = -185.3936 numIt = 0030

Try Matrix ALPS

%Run it if requested
if tryMatrixAlps

    %Notify
    disp('Starting Matrix ALPS')

    %Specify options

    % ALPS parameters
    Alpsparams.ALPSiters = 1500;         % Maximum number of iterations
    Alpsparams.tol = opt.tol;              % Convergence tolerance
    Alpsparams.xpath = 0;               % Keep history log
    Alpsparams.svdMode = 'propack';     % SVD method - default mode for Matrix ALPS II - other options: 'svds', 'svd'
    Alpsparams.cg_tol = 1e-10;          % Conjugate gradients tolerance
    Alpsparams.cg_maxiter = 500;        % Maximum number of conjugate gradient iterations
    Alpsparams.svdApprox = 0;           % Set to 1 for column subset selection - really slow...
    Alpsparams.power = 2;               % Number of iterations in subspace range finder
    Alpsparams.params.tau = 0;


    %Build operators
    [ix,iy] = find(omega);
    %linearInd = sub2ind([M L], double(ix), double(iy));
    tlinearInd = sub2ind([L M], double(iy), double(ix));
    %idx = linearInd(:);
    tidx = tlinearInd(:);
    %Aop = @(z) z(idx);
    %At = @(z) full(sparse(double(ix), double(iy), z, M, L));
    tA = @(z) z(tidx);
    tAt = @(z) full(sparse(double(iy), double(ix), z, L, M));

    %Define yt
    yt = tA(Y');
    %y = Aop(Y);

    %Call it
    tstart = tic;
    [X_hat3, numiter3, X_path3,estHistMatrixAlps,timingMatrixAlps] =...
        matrixALPSII_QR_timing(yt, tA, tAt, L, M, N, Alpsparams, [],error_function); %#ok<ASGLU>
    tMatrixAlps = toc(tstart);

%     tstart = tic;
%     [X_hat2, numiter2, X_path2] = matrixALPSII(y, Aop, At, M, L, N, Alpsparams, Z);
%     tMatrixAlpsII = toc;

    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'Matrix ALPS';
    results{loc}.err = estHistMatrixAlps.errZ(end);
    results{loc}.time = tMatrixAlps;
    results{loc}.errHist = estHistMatrixAlps.errZ;
    results{loc}.timeHist = timingMatrixAlps;


end

Starting Matrix ALPS

Try Grouse

if tryGrouse
    disp('Starting GROUSE')
    %Specify grouse options
    step_size = 0.5; %used to use 0.1, then increased to 1.0
    maxCycles = 600;
    maxrank = N;

    %Build the inputs
    [I,J] = find(omega);
    S = reshape(Y(omega),[],1);

    %Call it
    tstart = tic;
    [~,~,~,timingGrouse,estHistGrouse] =...
        grouse_timing(I,J,S,M,L,maxrank,step_size,maxCycles,opt.tol,error_function);
    tGrouse = toc(tstart);


    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'GROUSE';
    results{loc}.err = estHistGrouse.errZ(end);
    results{loc}.time = tGrouse;
    results{loc}.errHist = estHistGrouse.errZ;
    results{loc}.timeHist = timingGrouse;

end

Starting GROUSE

Try VBMC

if tryVbmc

    options.verbose = 0;
    options.MAXITER = 2000;
    options.DIMRED = 0; % Reduce dimensionality during iterations?
    % you can also set the threshold to reduce dimensions
    % options.DIMRED_THR = 1e3;
    %Estimate noise variance? (beta is inverse noise variance)
    %options.UPDATE_BETA = 1;
    % options.UPDATE_BETA_START = 1;% iteration number to start estimating noise variance
    % If the noise inv. variance is not to be estimated, set
    options.UPDATE_BETA = 0; % and set beta using
    options.beta = 1e9;
    % Manually tuning this parameter can give significantly better results.

    % options.initial_rank = 'auto'; % This sets to the maximum possible rank
    options.initial_rank = N; % or we can set a value.
    %options.init = 'rand';



    %Run it
    disp('Starting VBMC');
    tstart = tic;
    [~,timingVbmc,estHistVbmc] = VBMC_timing(omega, Y, options,error_function);
    tVbmc = toc(tstart);


    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'VSBL';
    results{loc}.err = estHistVbmc.errZ(end);
    results{loc}.time = tVbmc;
    results{loc}.errHist = estHistVbmc.errZ;
    results{loc}.timeHist = timingVbmc;


end

Starting VBMC

Try LMaFit

if tryLmafit

    %Inform user
    disp('Starting LMaFit')

    %Get input data
    Known = find(omega);
    data = reshape(Y(omega),[],1);

    %Options
    Lmafit_opts.est_rank = 0; %fixed rank
    Lmafit_opts.tol = opt.tol;
    Lmafit_opts.print = 0; %no printout
    Lmafit_opts.maxit = 6000;
    Lmafit_opts.init = 0; %Normally leave this off
    Lmafit_opts.X = Ahat;
    Lmafit_opts.Y = xhat;

    %Do it
    tstart = tic;
    [~,~,~,timingLmafit,estHistLmafit] =...
        lmafit_mc_adp_timing(M,L,N,Known,data,Lmafit_opts,error_function);
    tLmafit = toc(tstart);


    %Save results
    loc = length(results) + 1;
    results{loc}.name = 'LMaFit';
    results{loc}.err = estHistLmafit.errZ(end);
    results{loc}.time = tLmafit;
    results{loc}.errHist = estHistLmafit.errZ;
    results{loc}.timeHist = timingLmafit;

end

Starting LMaFit

Try inexact ALM

if tryInexactAlm
    disp('Starting Inexact ALM')

    try
        %Call it
        tstart = tic;
        %[~,~,~,timingInexactAlm,estHistInexactAlm] =...
        %   inexact_alm_mc_timing(sparse(Y),opt.tol,300,error_function);
        [~,~,~,timingInexactAlm,estHistInexactAlm] =...
            inexact_alm_mc_tasos_timing(sparse(Y),opt.tol,2000,N,error_function);
        tInexactAlm = toc(tstart);



        %Save results
        loc = length(results) + 1;
        results{loc}.name = 'Inexact ALM';
        results{loc}.err = estHistInexactAlm.errZ(end);
        results{loc}.time = tInexactAlm;
        results{loc}.errHist = estHistInexactAlm.errZ;
        results{loc}.timeHist = timingInexactAlm;

    catch %#ok<CTCH>
        %Save results
        loc = length(results) + 1;
        results{loc}.name = 'Inexact ALM';
        results{loc}.err = inf;
        results{loc}.time = inf;
        results{loc}.errHist = inf;
        results{loc}.timeHist = inf;

    end
end

Starting Inexact ALM

Store the options structures in results

results{1}.optIn = optIn;

Show Results

if nargin == 0

    %Show error plots
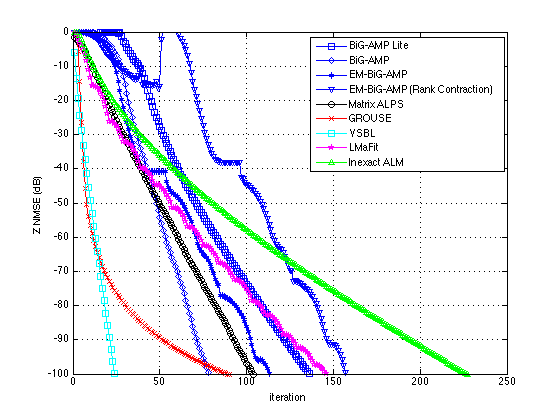
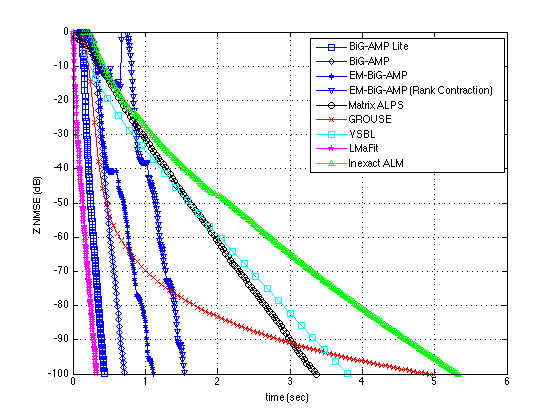
    plotUtilityNew(results,[-100 0],200,201)

    %Display
    results{:} %#ok<NOPRT>

end

ans = 

        name: 'BiG-AMP Lite'
         err: -127.8798
        time: 1.6713
     errHist: [176x1 double]
    timeHist: [176x1 double]
       optIn: [1x1 struct]


ans = 

        name: 'BiG-AMP'
         err: -143.9354
        time: 1.6218
     errHist: [105x1 double]
    timeHist: [105x1 double]


ans = 

        name: 'EM-BiG-AMP'
         err: -152.8152
        time: 2.6799
     errHist: [168x1 double]
    timeHist: [168x1 double]


ans = 

        name: 'EM-BiG-AMP (Rank Contraction)'
         err: -185.3936
        time: 3.7089
     errHist: [238x1 double]
    timeHist: [238x1 double]
        rank: 10


ans = 

        name: 'Matrix ALPS'
         err: -148.1998
        time: 6.5163
     errHist: [155x1 double]
    timeHist: [155x1 double]


ans = 

        name: 'GROUSE'
         err: -118.5300
        time: 22.2990
     errHist: [247x1 double]
    timeHist: [247x1 double]


ans = 

        name: 'VSBL'
         err: -134.5088
        time: 5.7639
     errHist: [34x1 double]
    timeHist: [34x1 double]


ans = 

        name: 'LMaFit'
         err: -149.7031
        time: 2.0092
     errHist: [247x1 double]
    timeHist: [247x1 double]


ans = 

        name: 'Inexact ALM'
         err: -131.2548
        time: 11.0982
     errHist: [328x1 double]
    timeHist: [328x1 double]


ans = 

  Columns 1 through 4

    [1x1 struct]    [1x1 struct]    [1x1 struct]    [1x1 struct]

  Columns 5 through 8

    [1x1 struct]    [1x1 struct]    [1x1 struct]    [1x1 struct]

  Column 9

    [1x1 struct]

Published with MATLAB® 7.14